How to convert decimal numbers into ASCII code? – an easy step-by-step ChatGPT guide

ASCII (American Standard Code for Information Interchange) is a widely used character encoding standard. It represents characters as decimal numbers, with each character assigned a unique code. The ASCII standard uses values ranging from 0 to 127 to represent a total of 128 characters.

To convert a decimal number into its corresponding ASCII code, you need to ensure that the decimal value falls within the range of 0 to 127. Here’s how the conversion process works:

1. Obtain the decimal number you want to convert into ASCII.

2. Verify that the decimal number is within the valid range of 0 to 127. If the number is outside this range, it cannot be directly represented as an ASCII code. In such cases, you may need to use an extended character encoding scheme like Unicode.

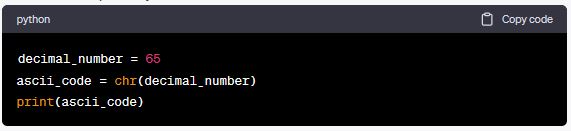
3. Once you have a valid decimal number, you can obtain its ASCII code by simply treating the decimal value as an integer. In most programming languages, this can be done using typecasting or conversion functions. For example, in Python, you can use the chr() function to convert a decimal number to its ASCII character representation.

   Here’s an example in Python:

   

   ChatGPT image

Output:

In this example, the decimal number 65 corresponds to the uppercase letter ‘A’ in ASCII.

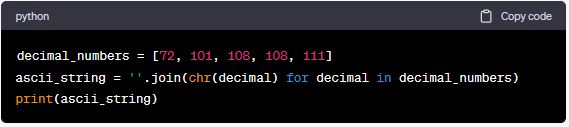
4. If you want to convert a sequence of decimal numbers into ASCII characters, you can repeat the conversion process for each number individually. For instance, if you have the decimal numbers [72, 101, 108, 108, 111], you can convert them into their corresponding ASCII characters to obtain the word “Hello”.

Here’s an example in Python:

Output:

In this example, each decimal number is converted to its corresponding ASCII character using the chr() function. The resulting characters are then joined together to form the string “Hello”.

That’s the basic process of converting decimal numbers into ASCII codes. It’s a straightforward operation that allows you to represent characters using their corresponding decimal values. Keep in mind that ASCII is limited to 128 characters, so certain characters or symbols may require alternative encoding schemes beyond the ASCII range.

+
*Additional Notes:

Now for those of you who would like to know more about decimal numbers:

Understanding Decimal Numbers in Mathematics

Decimal numbers are a fundamental concept in mathematics, widely used in everyday life for representing and working with fractional quantities. Whether you’re calculating the price of groceries, measuring distances, or dealing with financial transactions, decimal numbers play a crucial role. In this article, we’ll explore what decimal numbers are, how they are represented, and how they are used in various mathematical operations.

Definition:

In mathematics, decimal numbers are a way of expressing real numbers using a base-10 number system. The term “decimal” comes from the Latin word “decimus,” meaning tenth. A decimal number consists of two main parts: an integer part and a fractional part separated by a decimal point. The integer part represents whole numbers, while the fractional part represents fractions or parts of a whole.

Decimal Notation:

The decimal system uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each digit’s position in a decimal number represents a power of 10. The digit at the rightmost position represents the units, the next position to the left represents tens, followed by hundreds, thousands, and so on.

For example, let’s consider the decimal number 123.456. The digit 1 is in the hundreds position, 2 is in the tens position, and 3 is in the units position. The fractional part has 4 in the tenths position, 5 in the hundredths position, and 6 in the thousandths position.

Decimal Fraction:

The fractional part of a decimal number represents a fraction or a part of a whole. Each digit in the fractional part has a value that is a power of 10, but with a negative exponent. The first digit after the decimal point represents tenths, the second digit represents hundredths, and so on.

Using our previous example, the decimal number 123.456 can be written as a fraction as follows: 123.456 = 123 + 4/10 + 5/100 + 6/1000

Operations with Decimal Numbers:

Decimal numbers can be added, subtracted, multiplied, and divided, just like whole numbers. The operations follow the same rules as arithmetic with whole numbers. When performing operations on decimal numbers, it’s important to align the decimal points correctly to maintain accuracy.

For example, let’s add 2.5 and 1.75:

Applications of Decimal Numbers:

Decimal numbers are widely used in various practical applications. They are used in financial calculations, measurements, scientific computations, and many other fields. Decimal numbers allow us to express precise quantities, such as money, measurements, and data, with accuracy up to the desired decimal places.

Conclusion:

Decimal numbers are an essential part of mathematics, providing a concise and flexible way to represent real quantities. With their ability to express both whole numbers and fractions, decimal numbers are versatile and widely used in various fields. Understanding decimal numbers and their operations is crucial for everyday calculations and advanced mathematical concepts alike.